miércoles, 11 de diciembre de 2013
EXAMEN PENDIENTES 1º BACHILLERATO FÍSICA Y QUÍMICA. Primera parte
Se convoca al alumnado de 2º de bachillerato con la asignatura Física y Química de 1º de bachillerato pendiente, a la prueba de los 8 temas de química que se realizará el jueves 23 de enero de 2014 en el Departamento de Física y Química a las 11,30h.
Los alumnos deben llevar una calculadora científica no programable.
El examen tendrá dos horas de duración.
Tal y como se establece en la programación del curso 13/14, la superación del examen no supondrá la recuperación de la asignatura, ya que en el mes de abril se realizará un examen de los temas correspondientes a la parte de física. Ambas pruebas deben alcanzar la calificación de 4, y el promedio entre ambas debe ser de 5 para superar la asignatura.
El el examen se basará en los documentos que se entregaron a los alumnos al principio de este curso.
Se atendrán todas las dudas y cuestiones que surjan en el Departamento de Física y Química.
En los Corrales del Buelna, a 11 de diciembre de 2013
lunes, 25 de noviembre de 2013
CIENCIA Y SERIES. SHELDON COOPER EN THE BIG BANG THEORY Y EL GATO DE SCHRÖDINGER

Al final de la primera temporada
de la popular serie The Big Bang Theory, Sheldon Cooper explica el experimento
del gato de Schrödinger para compararlo con la situación sentimental de Penny y
Leonard.
Cuando se habla del "gato de
Schrödinger" se hace referencia a la paradoja que surge de un
célebre experimento imaginario propuesto por Erwin Schrödinger en el año 1937
para observar las diferencias entre interacción y medida en el campo de la
mecánica cuántica.
El experimento mental consiste en
imaginar a un gato dentro de una caja que también contiene un peligroso dispositivo formado por una ampolla de vidrio
que contiene un veneno muy volátil y por un martillo sujeto sobre la ampolla de
forma que si cae sobre ella la rompe y se escapa el veneno con lo que el gato
moriría. El martillo está conectado a un mecanismo detector de partículas alfa;
si llega una partícula alfa el martillo cae rompiendo la ampolla con lo que el
gato muere, por el contrario, si no llega no ocurre nada y el gato continua
vivo.
Al lado del detector se sitúa un átomo
radiactivo con unas determinadas características: tiene un 50% de
probabilidades de emitir una partícula alfa en una hora.
Evidentemente, al cabo
de una hora habrá ocurrido uno de los dos sucesos posibles: el átomo ha emitido
una partícula alfa o no la ha emitido (la probabilidad de que ocurra una cosa o
la otra es la misma). Como resultado de la interacción, en el interior de la
caja, el gato está vivo o está muerto. Pero no podemos saberlo si no la abrimos
para comprobarlo.
Si lo que ocurre en el interior
de la caja lo intentamos describir aplicando las leyes de la mecánica cuántica,
llegamos a una conclusión muy extraña. El gato vendrá descrito por una función
de onda resultado de la superposición de dos estados
combinados al cincuenta por ciento: "gato vivo" y "gato muerto".
Es decir, aplicando el formalismo cuántico, el gato estaría a la vez vivo y
muerto; se trataría de dos estados indistinguibles.
La única forma de averiguar qué
ha ocurrido con el gato es realizar una medida: abrir la caja y mirar dentro.
En unos casos nos encontraremos al gato vivo y en otros muerto. Al realizar la medida, el observador interactúa con el sistema y lo
altera, rompe la superposición de estados y el sistema se decanta por uno de
sus dos estados posibles.
El sentido común nos indica que
el gato no puede estar vivo y muerto a la vez. Pero la mecánica cuántica dice
que mientras nadie mire en el interior de la caja el gato se encuentra en una
superposición de los dos estados: vivo y muerto.
Esta superposición de estados es
una consecuencia de la naturaleza ondulatoria de la materia y su aplicación a
la descripción mecanocuántica de los sistemas físicos, lo que permite explicar
el comportamiento de las partículas elementales y de los átomos. La aplicación
a sistemas macroscópicos como el gato o, incluso, si así se prefiere, cualquier
profesor de física, nos llevaría a la paradoja que nos propone Schrödinger
Al final de la primera temporada
de la popular serie The Big Bang Theory, Sheldon Cooper explica el experimento
del gato de Schrödinger para compararlo con la situación sentimental de Penny y
Leonard.
Leonard finalmente reúne el
coraje suficiente para invitar a Penny a salir. Penny no está acostumbrada a
salir con tipos como Leonard y eso pudo ocasionar que sus relaciones anteriores
no hayan funcionado, pero por otro lado si esta relación no termina bien, se
arriesgaría a perder un buen amigo.
Penny le pide algún consejo a
Sheldon porque debería conocer a Leonard más que al resto. Sheldon le da la
solución de considerar al gato de Schrodinger. Penny confunde Schrodinger con
la vecina del apartamento 2A pero Sheldon la corrige de inmediato diciéndole
que esa es la Señorita Grossinger, y le comienza a explicar que en 1935, Erwin
Schrödinger, en un intento de explicar la interpretación de la física cuántica
de Copenhague, propuso un experimento donde un gato es situado dentro de una
caja con conductos de veneno que serian abiertos en un momento aleatorio y como
nadie sabe cuándo o si el veneno se ha introducido, hasta que la caja se
abriese, el gato puede ser considerado tanto vivo como muerto.
Penny no entendió la explicación
y Sheldon le responde que eso es porque aún no terminaba de explicar. Sheldon
continua diciendo que simplemente el gato de Schrodinger es la potencial
relación que tiene ella con Leonard ahora mismo, puede ser pensada tanto como
mala y como buena, y que solo abriendo la caja se puede averiguar cuál es.
Con ayuda del artículo de M.A. Gómez
LA REALIDAD EXISTE DE DOS MODOS: DUALIDAD DE LA LUZ
La luz atravesando el objetivo de una cámara fotográfica se comporta como una onda.
 Pero en el instante siguiente, cuando golpea la película, pierde el aspecto de onda y se manifiesta el caracter corpuscular de los fotones.
Pero en el instante siguiente, cuando golpea la película, pierde el aspecto de onda y se manifiesta el caracter corpuscular de los fotones.
Jamás la luz manifestará dos aspectos del mismo hecho.
La realidad posee dos modos de existir que no pueden manifestarse a la vez en la misma acción.
Este es el PRINCIPIO DE INCERTIDUMBRE DE HEISEMBERG
martes, 3 de septiembre de 2013
MARIE CURIE Y EL RADIO LETAL
 Marie Curie no solo fue la primera mujer en recibir un
premio Nobel y la única en recibir dos, sino que además fue la primera mujer
licenciada en Ciencias en la Sorbona de París, la primera en doctorarse en
Ciencias en Francia y la primera en tener una cátedra.
Marie Curie no solo fue la primera mujer en recibir un
premio Nobel y la única en recibir dos, sino que además fue la primera mujer
licenciada en Ciencias en la Sorbona de París, la primera en doctorarse en
Ciencias en Francia y la primera en tener una cátedra.
Además fue la primera mujer enterrada en el Panteón de los
Hombres Ilustres de Francia (sus restos fueron trasladados allí en 1995, aunque
su muerte se había producido muchos años antes).
Recibió su Premio Nobel de Física en 1903, conjuntamente con
su marido, Pierre Curie, y otro en 1911, en solitario, de Química.
En toda la historia sólo ha habido otras tres personas que
hayan recibido dos Premios Nobel: Linus Pauling, Frederik Sanger y John
Bardeen. De ellos solo Linus Pauling recibió dos premios Nobel en dos
categorías distintas, uno de ellos de Química y otro de la Paz.
La proeza de Marie Curie es extraordinaria, teniendo en
cuenta que el Premio Nobel lo han recibido hasta el día de hoy 786 hombres y
solo 44 mujeres.
Si queremos explicarnos en términos sencillos, po
demos decir
que Marie Curie descubrió el polonio, el radio, y logró “medir” la
radiactividad (descubrió un nuevo método para descubrir elementos midiendo su
radiactividad).
Podemos hacernos una idea de la sociedad machista de la
época, al ver que en el año 1903, cuando Marie y Pierre recibieron el Nobel,
sólo le dieron al matrimonio el dinero correspondiente a una persona (setenta
mil francos), mientras que Becquerel, que también ganó el Nobel ese año, se
llevó el dolo setenta mil. Y en la entrega de galardones fue Pierre quien subió
al estrado y dio un discurso, mientras que ella se quedaba sentada entre el
público (aunque Pierre le atribuyó a Marie todo el mérito del descubrimiento
del radio y del polonio).
La Academia de Ciencia rechazó la candidatura de Marie Curie
en 1911.
Marie Curie era polaca, y en su época, en la Polonia
ocupada, las niñas no podían cursar estudios universitarios. Por suerte, Marie
llegó a un acuerdo con su hermana mayor. Mientras su hermana estudiaba Medicina
en Francia, Marie trabajaría como institutriz para pagarle los estudios. Y
luego, cuando la hermana mayor se licenciara, serie ella quien le pagaría sus
estudios a Marie Curie. Así lo hicieron. Marie Curie se licenció en Física,
número uno de su promoción.
 Conoció a Pierre Curie, se casaron, y comenzaron sus
investigaciones. Pierre Curie soñó toda su vida con tener un laboratorio, pero
no lo lograba, y el descubrimiento del polonio y del radio se dieron en un
viejo cobertizo.
Conoció a Pierre Curie, se casaron, y comenzaron sus
investigaciones. Pierre Curie soñó toda su vida con tener un laboratorio, pero
no lo lograba, y el descubrimiento del polonio y del radio se dieron en un
viejo cobertizo.
Los trabajos de la pareja se basaron en un descubrimiento
previo de Becquerel: Algunos elementos como el uranio, emiten unas radiaciones
invisibles altamente energéticas.
Ya se sabía, que estos rayos tenían la propiedad de que el
aire de alrededor se volviera conductor de la electricidad, y Marie se ocupó de
medir la conductividad del aire con un espectrómetro piezoeléctrico de cuarzo
que había inventado su marido Pierre.
Marie vio que la pecblenda, el mineral del que se extrae el
uranio, electrizaba más el aire de alrededor que el propio uranio puro extraído
de ella. Y concluyó, que en el mineral debía haber algún otro elemento más
radiactivo que el uranio.
 Ese elemento era el radio, y debieron procesar diez
toneladas de pecblenda para extraer un decigramo de cloruro de radio. Todo ello
lo hicieron en las penosas condiciones de su cobertizo, con un cubo lleno de
mineral hirviente y un palo de hierro para remover la mezcla.
Ese elemento era el radio, y debieron procesar diez
toneladas de pecblenda para extraer un decigramo de cloruro de radio. Todo ello
lo hicieron en las penosas condiciones de su cobertizo, con un cubo lleno de
mineral hirviente y un palo de hierro para remover la mezcla.
¿Y qué es el radio? Es un elemento, que en su forma oxidada
(cloruro de radio) es azulado, luminoso, bello y asesino.
¿Para qué se usa hoy el radio?
- Cuando se mezcla con berilio, es una fuente de neutrones para experimentos físicos.
- El cloruro de radio se usa en medicina para producir radón, que se usa en tratamientos contra el cáncer.
- Una unidad de radiactividad, el curio, está basada en la radiactividad del radio-226.
- Radioisótopos descubiertos recientemente, como los de cobalto-60 y cesio-137, están reemplazando al radio incluso en estos limitados usos, dado que son más potentes y más seguros de manipular.
También encontraron polonio. El polonio es cuatrocientas
veces más radiactivo que el uranio. Y el radio es tres mil veces más radiactivo
que el uranio.
La gente se volvió loca con el descubrimiento. ¡El radio se
incluía en las cremas faciales, en dentífricos para blanquear los dientes, o en
pomadas para vencer la celulitis!
Se suponía que los varones impotentes se curaban con el
radio, que los baños radiactivos curaban la neumonía… y así durante treinta
años. Fue a partir de 1925 cuando la gente comenzó a sospechar de este
elemento, cuando un famoso campeón de golf empezó a tomar todos los días una
disolución de radio para curar un dolor en el brazo. Al principio decía que se
sentía más joven, pero ocho años después murió con los huesos de la mandíbula y
del cráneo deshechos.
Marie narra en su diario como las sustancias radiactivas
impregnan todos los objetos del laboratorio, cómo vuelven radiactivo el polvo
del aire del laboratorio, y las ropas de los investigadores. Por poner un
ejemplo, en 1956 se mide la radiactividad de los cuadernos de notas de 1902 de
los Curie, y se observa que aún están fuertemente contaminados.
 |
| Cloruro de Radio |
Pierre muere en 1906, con cuarenta y siete años, aplastado
por un carro, pero Pierre ya estaba muy enfermo. Sufría un gran agotamiento y
fuertes crisis de dolor, porque la radiactividad le estaba deshaciendo el
esqueleto. Pero ellos no lo sospechaban, y nunca pensaron en implantar medidas
de seguridad en su laboratorio. De hecho, hay una foto en que Marie y su hija
Irene, aspiran sustancias con la por medio de una pipeta. En 1931 (cuando su
laboratorio llevaba años trabajando con radio), un tercio de los trabajadores
del instituto mostraban anomalías en la sangre, porque la radiactividad ataca
los glóbulos rojos. Además, a los científicos les gustaba llevar un tubito de
radio activo en el bolsillo del chaleco, por orgullo, y por su azulado fulgor. Y
el matrimonio tenía un tubo de radio sobre el cabecero de la cama para
disfrutar de su fulgor azulado.
En su propio diario narra Marie Curie las pérdidas de piel
en los dedos de las manos que han sostenido tubos con radio, habla de dolorosas
úlceras y un extraño dolor profundo que no desaparece con las heridas. A los
sesenta años Marie parecía una anciana de ochenta, sufrió mucho dolor en sus
últimos días, y se quedó ciega. Murió de anemia perniciosa a los sesenta y
siete años. Incluso Irene, su hija también científica y ganadora de un Nobel en
1938 por descubrir la radiactividad artificial, murió de leucemia a los
cincuenta y nueve años.
Entonces Marie se dedicó a investigar el estudio de la
medición de las sustancias radiactivas, y definió un patrón internacional
llamado curio. Y además, logró obtener radio puro (hasta ahora solo había
conseguido cloruro de radio), y todo por las críticas que Lord Kelvin (famoso
físico y matemático de la época), había vertido sobre ella en el periódico The
Times. Marie obtuvo radio puro, de color blanco brillante, que se oxidaba
rápidamente con el oxígeno del aire.
Se le atribuyen otras proezas además de las descritas, por
ejemplo, en 1914, cuando ya había ganado los dos premios Nobel, y estallaba la
Primera Guerra Mundial, cargó con las reservas de radio de Francia, que pesaban
unos treinta kilos, y las llevó en tren de París a Burdeos, para que no se
apropiaran de ellas los alemanes, estando ya enferma y fatigada. Además lideró
un proyecto para colocar máquinas de rayos X de los laboratorios y
universidades francesas, en unidades móviles para recorrer el país durante la
guerra.
Dijo Soddy, un importante científico de la época, que elmejor descubrimiento que hizo Pierre Curie fue a Marie Curie, y el mejor descubrimiento que hizo ella, fue la radiactividad.
Bibliografía:
"La ridícula idea de no volver a verte", Rosa Montero
"Marie Curie Genio Obsesivo", barbara Goldsmith
"Curie", Sarah Dry
"Marie Curie y su tiempo", Jose Manuel Sánchez Ron
viernes, 21 de junio de 2013
CALENDARIO EXÁMENES SEPTIEMBRE. DEPARTAMENTO DE FÍSICA Y QUÍMICA
Martes 3 de Septiembre de 2013
- 1º bachillerato Física y Química pendientes 11,30 h- 13,00 h
- 2º bachillerato Química 13,00 h- 14,20 h
Miércoles 4 septiembre de 2013
- 3º ESO Física y Química* 10,00 h- 11,30 h
- 4º ESO Física y Química* 10,00 h- 11,30 h
- 1º Bachillerato Física y Química 10,00 h- 11,30 h
- 2º Bachillerato Física 10,00 h- 11,30 h
Se recuerda a todos los alumnos que deben acudir con calculadora.
Los alumnos de física de 2º de bachillerato deberán traer también compás, y reglas.
*Alumnado de la ESO:
Se recuerda a los alumnos de 3º y 4º de ESO, que el examen extraordinario de septiembre tiene un peso del 80% en la nota final.
Un 10% se calcula con la nora ordinaria del curso, y el otro 10% restante con los trabajos y ejercicios que se han entregado a los alumnos con las notas de junio.
Por ello EL DÍA DEL EXAMEN DE SEPTIEMBRE, ANTES DE COMENZAR EL MISMO, LOS ALUMNOS SUSPENSOS ENTREGARÁN A SU PROFESORA LOS EJERCICIOS RESUELTOS.
NO SE ADMITIRÁN EJERCICIOS EN OTRAS FECHAS U HORAS. LA FECHA Y HORA DE ENTREGA SON LAS DEL EXAMEN EXTRAORDINARIO.
lunes, 17 de junio de 2013
3º ESO. CONVOCATORIA EXTRAORDINARIA SEPTIEMBRE
CRITERIOS PARA LA EVALUACIÓN
EXTRAORDINARIA
FÍSICA Y QUÍMICA 3º ESO
Los
alumnos suspensos dispondrán de una prueba extraordinaria. Dicho
examen versará sobre los aspectos curriculares mínimos que se
consideran básicos para superar la asignatura. El examen contendrá
preguntas teóricas, cuestiones y problemas; valorados sobre diez
puntos.
En el contexto de
evaluación continua si el alumno supera la prueba extraordinaria,
superará la materia.
Sin perjuicio de lo
anterior, la calificación final extraordinaria se
obtendrá ponderando al 80% la calificación de la prueba, al 10% la
valoración de la evolución del alumno durante las evaluaciones
ordinarias, y al 10% la valoración de las
actividades de recuperación y refuerzo.
Prueba
extraordinaria de septiembre
La
prueba contendrá ejercicios con contenidos mínimos de los 6 temas
impartidos a lo largo del curso.
Los alumnos estudiarán con el
cuaderno que se ha ido elaborando a lo largo del curso y con el libro
de texto, ya que los ejercicios y cuestiones del examen final
extraordinario serán similares a los realizados en clase.
Actividades
de recuperación y refuerzo
A
continuación se adjuntan los ejercicios de recuperación y refuerzo.
El
alumno deberá entregar el día del examen extraordinario de
septiembre la resolución de las fichas.
Las resoluciones de
los ejercicios serán razonadas. Todos los resultados llevarán sus
correspondientes unidades.
Se valorará
positivamente la realización de esquemas, la limpieza, y las
explicaciones coherentes y claras.
4º ESO. CONVOCATORIA EXTRAORDINARIA SEPTIEMBRE
CRITERIOS PARA LA EVALUACIÓN
EXTRAORDINARIA
FÍSICA Y QUÍMICA 4º ESO
Los
alumnos suspensos dispondrán de una prueba extraordinaria. Dicho
examen versará sobre los aspectos curriculares mínimos que se
consideran básicos para superar la asignatura. El examen contendrá
preguntas teóricas, cuestiones y problemas; valorados sobre diez
puntos.
En el contexto de
evaluación continua si el alumno supera la prueba extraordinaria,
superará la materia.
Sin perjuicio de lo
anterior, la calificación final extraordinaria se
obtendrá ponderando al 80% la calificación de la prueba, al 10% la
valoración de la evolución del alumno durante las evaluaciones
ordinarias, y al 10% la valoración de las
actividades de recuperación y refuerzo.
Prueba
extraordinaria de septiembre
La
prueba contendrá ejercicios con contenidos mínimos de los 9 temas
impartidos a lo largo del curso. Los alumnos estudiarán con el
cuaderno que se ha ido elaborando a lo largo del curso y con el libro
de texto, ya que los ejercicios y cuestiones del examen final
extraordinario serán similares a los de las 9 fichas.
1.-
Sistema periódico y enlace. (Tema 11 libro texto)
2.-
Formulación química inorgánica. (Anexo)
3.- El
carbono. Química orgánica. Formulación (Temas 14 y 15 libro texto)
4.-
La reacción química. Cálculos químicos. (Temas 12 y 13 libro texto)
5.- Cinemática. Movimiento. (Temas 1 y 2 libro texto)
6.-
Dinámica. Fuerzas. (Temas 3 y 4 libro texto)
7.-
Fuerza y presión en los fluidos. (Tema 5 libro texto)
8.-
Energía, trabajo y potencia (Temas 7 y 8 libro texto)
9.-
Energía térmica. Calor. (Tema 9 libro texto)
Actividades
de recuperación y refuerzo
A
continuación se adjuntan las 9 fichas correspondientes a cada uno de
los 9 temas del curso (son las mismas fichas que se han ido entregando al alumnado a lo largo del curso).
El
alumno deberá entregar el día del examen extraordinario de
septiembre, la resolución de 7 ejercicios de cada ficha, elegidos
por él mismo. Es decir, el alumno entregará resueltos 63
ejercicios.
Las resoluciones de
los ejercicios serán razonadas. Todos los resultados llevarán sus
correspondientes unidades.
Se valorará
positivamente la realización de esquemas, la limpieza, y las
explicaciones coherentes y claras.
EXAMEN FINAL ORDINARIO. 1º BACHILLERATO
 Curso 2012/2013 IES Javier Orbe Cano
Curso 2012/2013 IES Javier Orbe Cano
Física y Química 1º Bachillerato. Examen final ordinario
17/6/2013
Quien supere
esta prueba tiene aprobada la asignatura.
Este examen se
aprueba con un 5.
Las resoluciones de los ejercicios serán razonadas. Todos
los resultados llevarán sus correspondientes unidades.
Se valorará positivamente la realización de esquemas, la
limpieza, y las explicaciones coherentes y claras.
Datos: Masas atómicas: Ca=40u.; Cl=35,5u. ; H=1u. ; O=16u. ; C=12u.
ALUMNO:
- Calcula la masa de agua que se debe añadir a 100 cm3 de un ácido clorhídrico de un 36,23% en masa, que tiene una densidad de 1,18 g/cm3 para obtener un ácido del 22,33% de HCl y densidad 1,115 g/cm3.
(2 puntos)
- Un ácido clorhídrico concentrado tiene una densidad de 1,18 g/cm3 y tiene un 36,2% de HCl. Calcula el volumen de solución concentrada que se necesita para preparar 1 dm3 de solución cuya concentración en masa sea de 10 g/dm3.
(1,5 puntos)
- Al echar unas gotas de ácido clorhídrico sobre un trozo de mármol se desprenden burbujas gaseosas de dióxido de carbono y además se forman agua y cloruro de calcio. Teniendo en cuenta que el mármol tiene un 97% de carbonato de calcio, y que el rendimiento de la reacción es del 80%, calcula la la cantidad de mármol necesaria para obtener 200 cm3 de dióxido de carbono medido a 22ºC y 105 Pa.
- Calcula la F del sistema de la figura, y la tensión del hilo. Datos: M=6 kg; m=2 kg; a=2 m/s2; Coeficiente rozamiento=0,4; alfa=30º. Se requiere claridad, orden y esquema de fuerzas.
(3 puntos)
- Las posiciones de dos móviles A y B en función del tiempo en segundos son:
rA=(5t-7)i+(t+8)j m
rB=(3t+9)i+(3t-10)j m
¿Chocarán los móviles?
(1 punto)
martes, 11 de junio de 2013
EXAMEN REPESCA 1º BACHILLERATO. PARTE FÍSICA
Física y Química 1º Bachillerato.
Examen global Física. 11/6/2013
Quien supere
esta prueba tiene aprobada la parte del curso correspondiente a los seis temas
de física. Aprobar este examen es condición necesaria pero no suficiente para
superar la asignatura en junio, pues el alumnado debe haber superado
previamente la parte correspondiente a los 8 temas de química.
Este examen se
aprueba con un 5.
Las resoluciones de los ejercicios serán razonadas. Todos
los resultados llevarán sus correspondientes unidades.
Se valorará positivamente la realización de esquemas, la
limpieza, y las explicaciones coherentes y claras.
Cada apartado vale 1 punto.
ALUMNO:
Un tractor
circula por la carretera a 30 km/h. Su
rueda trasera tiene 1,8m de diámetro
y la delantera tiene 1m de diámetro.
El granjero observa un obstáculo, pisa el freno, y el tractor tarda 8 s en detenerse.
a. Calcula las
revoluciones por minuto de las dos ruedas antes de empezar a frenar.
b. Calcula la velocidad angular de la rueda trasera y su aceleración
normal a los 5 segundos de comenzar
a frenar.
c. Número de vueltas que da la rueda delantera desde que el granjero comienza a frenar,
hasta que el tractor se detiene.
Un perro
corre detrás del tractor. El tractor arrastra un remolque de 1m de altura, y el perro aprovecha que
el tractor se ha detenido para saltar al interior del remolque, cuando se
encuentra a 5m de distancia del
mismo. Si el salto tiene una inclinación de 35º respecto de la horizontal
d. Calcula a qué velocidad debe saltar el perro para caer dentro del
remolque.
Cuando el
perro entra en el remolque, el granjero arranca de nuevo, y comienza a
granizar. Las nubes están a 400 m de altura.
e. Calcula la velocidad que lleva un granizo cuando se estrella en la
cabeza del perro (no olvides que el remolque tiene 1m de altura y el perro 40 cm.
Uno de los
granizos, de 2 g de masa, al
caer verticalmente a 15 m/s, se
estrella con un escarabajo volador que viaja horizontalmente por el cielo a 7 m/s.
f. Calcula la masa del
escarabajo, sabiendo que tras el choque el granizo se ha desviado 30º de su trayectoria inicial vertical
y se queda pegado al escarabajo (tras el choque ambos van unidos con la misma
trayectoria). Explica qué principio o principios empleas para resolver este
apartado.
El tractor
tiene una masa de 2t.
g. Ignorando la masa del perro que viaja en el remolque, calcula la
fuerza que debe desarrollar el motor, para ascender con una aceleración a=1,5
m/s2 por una pendiente de 15º sin rozamiento.
El tractor
llega a una granja. El granjero tiene almacenados miles de paquetes de alfalfa
para sus caballos. El granjero es muy ingenioso, y ha ideado un sistema como el
de la figura 1 para bajar los paquetes de alfalfa de un
altillo, de modo que la velocidad de caída sea amortiguada por un resorte.
h. Calcula por consideraciones
energéticas la deformación que sufre el resorte de la figura 1, sabiendo
que a=40º, la masa del paquete
de alfalfa m=1 kg, k=400 N/m y d=4m.
El
granjero es tan ingenioso, y se siente tan capaz, que ha decidido sacarse el
bachillerato a distancia. Estudia en su casa todas las noches después de dar de
comer a sus caballos. Se sienta a repasar antes de su examen de repesca de
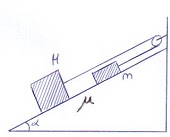
física y química de 1º de bachillerato, y trata de resolver un ejercicio que
aparece en la figura 2.
i.
Calcula la aceleración
del sistema en función de M, m, alfa y el coeficiente de rozamiento, trabajando como si estas cuatro
magnitudes fueran datos conocidos. (Se valorará el esquema de las fuerzas que
participan en el sistema)
j.
Calcula la tensión de
la cuerda.
 |
| FIGURA 1 |
 |
| FIGURA 2 |
SOLUCIONES
A)
Debes asumir que las dos ruedas llevan la misma velocidad
lineal, pero que la velocidad angular es diferente (por ser distinto el radio).
La velocidad angular de
la rueda pequeña, como es lógico, debe ser mayor.
Asumiendo
que v=w.R obtenemos las velocidades angulares. Y de rad/s pasamos a rpm
teniendo en cuenta que cada revolución son 6,28 radianes.
Los resultados son de
87,8 rpm y 158,5 rpm respectivamente
B)
La rueda delantera pasa de tener una velocidad angular de
9,2 rad/s a 0 rad/s en 8 segundos. Moviendo Circular Uniformemente Acelerado.
Por eso podemos calcular que la aceleración angular es de 1,15 rad/s2.
Con esa
aceleración angular podemos calcular que la velocidad angular de los 5 segundos
de comenzar a frenar es de 3,45 rad/s, y la velocidad lineal correspondiente es
de 3,1 m/s.
La aceleración normal
correspondiente es de 10,6 m/s2. debes tener cuidado, porque la aceleración
normal varía con el tiempo cuando tenemos un movimiento circular uniformemente
acelerado (MCUA).
C)
Con la ecuación del movimiento circular uniformemente
acelerado, podemos deducir que en los 8 segundos que dura la frenada, el giro
de la rueda delantera es de 96 radianes. Eso equivale a 15,3 vueltas.
D)
El perro realiza un movimiento en 2 dimensiones (tiro
parabólico). En el eje X no hay fuerzas externas que alteren la velocidad
inicial del perro (v.cos35), por tanto tenemos MRU.
En el eje
Y la aceleración de la gravedad va haciendo que la componente Y de la velocidad
inicial (v.sen35) del perro vaya disminuyendo con el tiempo (MRUA). Por eso,
aplicando las ecuaciones, considerando que la Y inicial del perro es 0 y la final es de 1m
(altura del remolque), y que en el eje X debe avanzar 5m:
t=0,71 s. v=8,6 m/s.
E)
El granizo baja en caída libre, sale de la nube con
velocidad inicial nula, y la gravedad hace que vaya acelerando. Su posición
inicial es y=400 m (en la nube), y al
final acaba en la cabeza del perro (y=1,4 m).
Con las ecuaciones del
MRUA obtenemos que t=9s, y que la velocidad del granizo al llegar al perro es
de -88,3 m/s.
F)
Al chocar el granizo con el escarabajo, se conserva el momento
lineal (principio de conservación del momento lineal).
Debemos plantearlo en
los dos ejes X e Y.
El momento lineal final
en X es de (m+0,002).v.sen30
En el eje Y es de
(m+0,002).v.cos.30, siendo v la velocidad final del granizo y el escarabajo que
van pegados, y m la masa del escarabajo que queremos calcular.
Planteando la
conservación del momento lineal en los dos ejes por separado, obtenemos dos
ecuaciones y dos incógnitas. Obtenemos que m=2,5.10-3 kg.
G)
En la dirección de la rampa hay dos fuerzas. La fuerza
motriz del motor del tractor y la componente del peso m.g.sen15. Aplicando la
2ª ley de Newton tenemos que F-m.g.sen15=m.a
De este modo despejamos
la fuerza motriz (Unos 35073N)
H)
Hemos de plantear un balance de energía, considerando que
toda la energía potencial del paquete de alfalfa se transforma en energía
potencial elástica cuando llega al resorte. m.g.h=1/2.K.x2.
Ha de tenerse en cuenta
que x es la deformación que sufre el resorte, y que h se puede obtener a partir
de d con la función trigonométrica seno, porque conocemos la inclinación de la
rampa (h=4.sen40)
X=0,35 m (Deformación)
I)
Hemos de asumir que el bloque M baja la rampa, y el bloque m
la sube. Ambos sufren un rozamiento que se opone al sentido de la marcha. Y no
hemos de olvidar las tensiones de los hilos. Aplicando la 2ª ley de Newton:
M.g.sen a -T+T-m.g.sen a- m.M.g.cos a-m.m.g.cosa=(M+m).a
Despejaríamos a
J)
Para calcular la
tensión de la cuerda, tenemos que aislar uno de los dos bloques.
M.g.sena-T-m-M-g-cosa=M.a Y despejamos la tensión T=g (sena-m.cosa)-a
Suscribirse a:
Comentarios (Atom)